What is Nuclear Fusion?
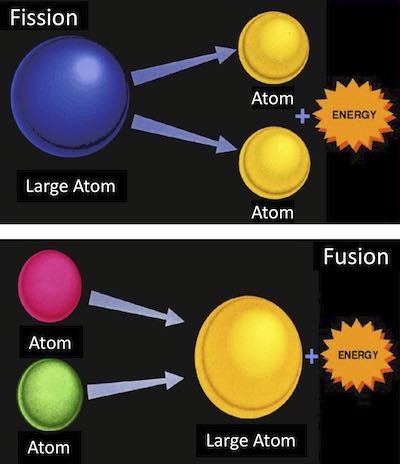
Nuclear fission and fusion are candidate sources of energy with sufficient energy density to supply the increasing world population with its steadily increasing energy demands. In a fission reaction, a heavy nucleus splits apart into smaller nuclei, as shown in Fig. 1 (top). Fission is a mature technology powering present nuclear power reactors. In a fusion reaction, on the contrary, two light nuclei stick together to form a heavier nucleus, as shown in Fig. 1 (bottom). Fusion is the source of virtually all the energy of the universe; the sun and stars shine due to fusion, supporting all life on Earth. Fossil and nuclear fuels are stored fusion energy. Like fission, fusion produces no air pollution or greenhouse gases. Unlike fission, fusion poses no risk of nuclear accident, no generation of high-level nuclear waste, and no generation of material for nuclear weapons. In addition, there is world-wide available, abundant supply of fuel, which would thus eliminate international tensions caused by imbalance in fuel supply. Unfortunately, controlled fusion is a very challenging technology and a nuclear-fusion power reactor is still not available. To provide energy from fusion is listed as one of the Engineering’s Grand Challenges by the US National Academy of Engineering. Scientists all around the world are working towards making nuclear-fusion energy a reality.
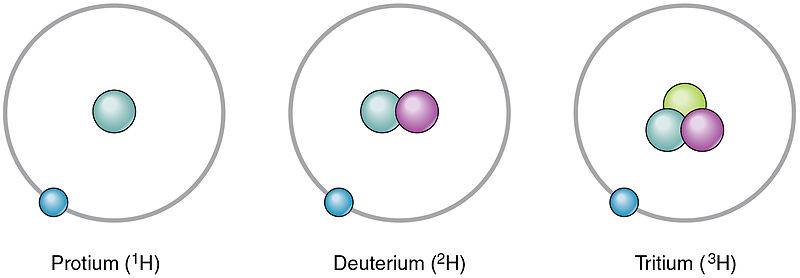
Hydrogen (1 proton + 1 electron) is the lightest element in the periodic table, which makes it a great candidate for fuel in a nuclear-fusion reactor. As shown in Fig. 2, Hydrogen has two isotopes (same number of protons (electrons), different number of neutrons): Deuterium and Tritium.
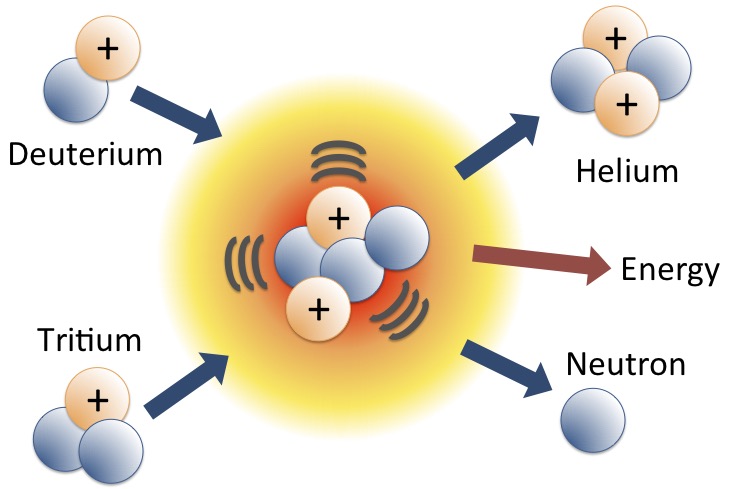
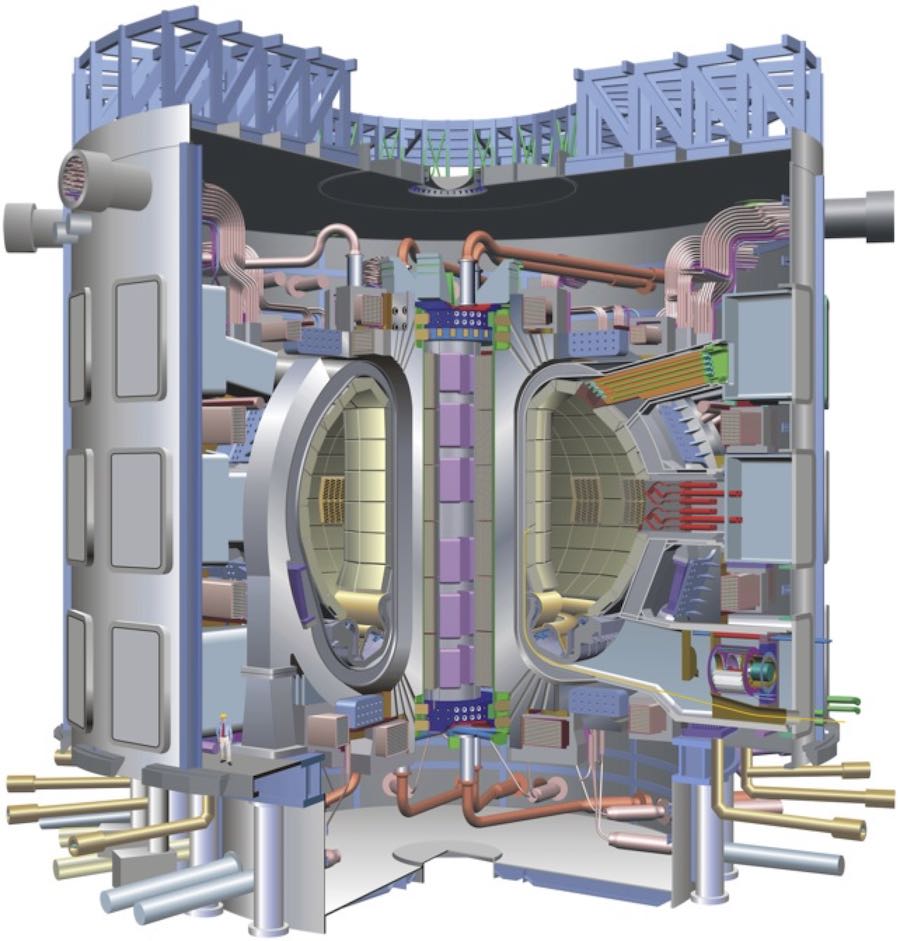
The first generation of nuclear-fusion reactors will be based on the deuterium (D) - tritium (T) reaction
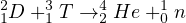
|
(1) |
where deuterium and tritium combine to form an isotope of helium (also known as alpha particle) plus an energetic neutron. This process is illustrated in Fig. 3.
In both fission and fusion reactions, the total masses after the reaction are less than those before. The “lost” mass appears as energy, with the amount given by the famous Einstein’ formula
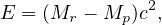
|
(2) |
where E is the energy, Mr is the mass of the reactant nuclei, Mp is the mass of the product nuclei, and c is the speed of light.
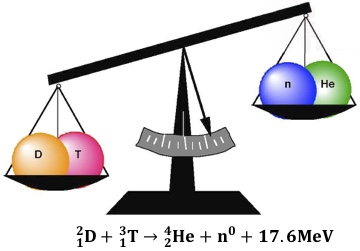
In the DT fusion reaction, as shown in Fig. 4, very small quantities of matter are converted into huge amounts of energy according to Einstein’s formula (2). The fraction of mass “lost” and converted into energy is just about 38 parts out of 10,000. Nevertheless, the fusion energy released from 1 gram of deuterium-tritium is equal to the energy from about 2,400 gallons of oil. The energy released by each DT fusion reaction is 17.6 MeV, which are carried as kinetic energy by the alpha particle (3.5 MeV or 1/5 of the total energy release) and the neutron (14.1 MeV or 4/5 of the total energy release).
What is the Fuel?
The major fuel, deuterium, may be readily extracted from ordinary water, which is available to all nations. The concentration of deuterium in water is 1 atom out of 6500 atoms of hydrogen. One pick-up truck full of deuterium would release the energy equivalent of approximately 2 million tons of coal (21,000 rail car loads), or 1.3 million tons of oil (10 million barrels), or 30 tons of Uranium Oxide (1 rail car load). Tritium does not occur naturally but would be produced from lithium, which is available from land deposits or from sea water which contains thousands of years’ supply (with a second-generation fusion concept using the D-D fusion reaction, the supply of deuterium in the seas would last for hundreds of millennia). The neutron resulting from the D-T nuclear reaction (1) will be combined with any two isotopes of lithium (36Li or 37Li) to produce the tritium required by the same D-T nuclear reaction:
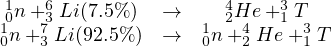
|
(3) |
The world-wide availability of these materials would thus eliminate international tensions caused by imbalance in fuel supply.
Why is Fusion so Difficult?
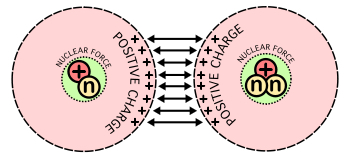
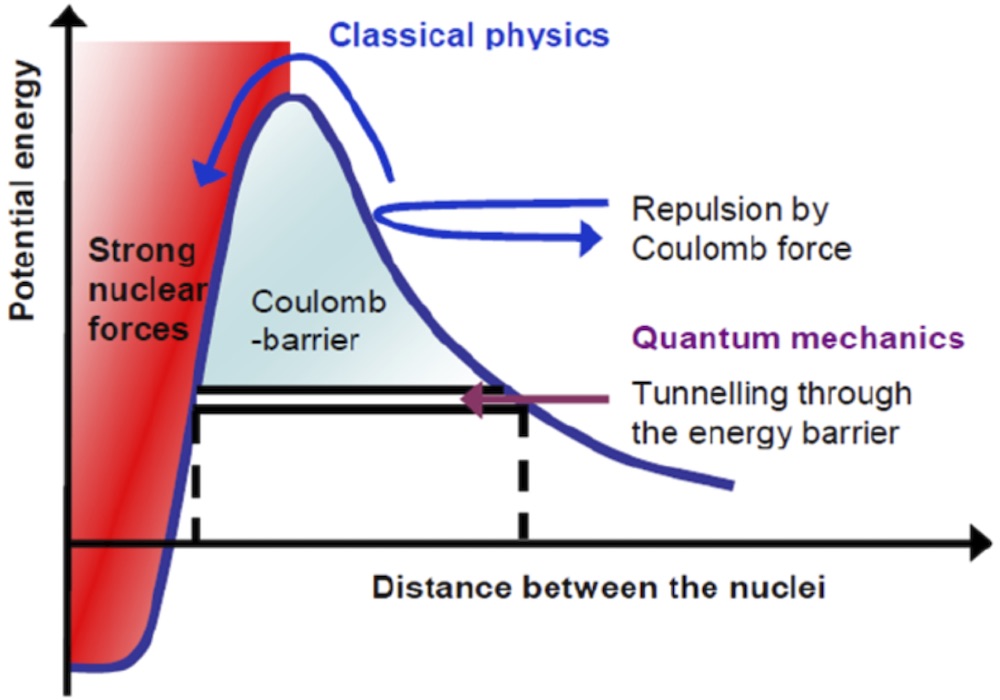
Since nuclei carry positive charges, they normally repel one another. Deuterium and tritium are not the exception as shown in Fig. 5. To overcome the Coulomb barrier, the kinetic energy of the nuclei is increased by heating. The higher the temperature, the faster the atoms or nuclei move.
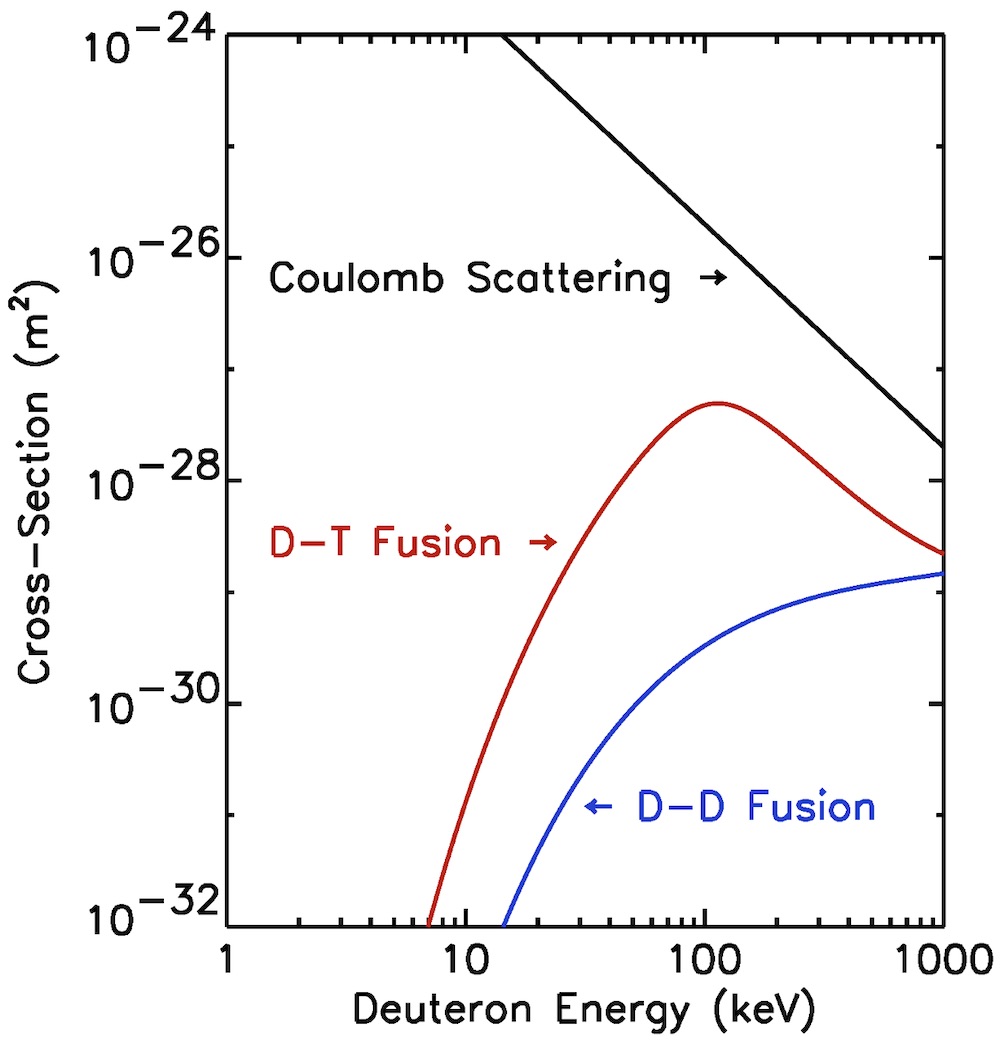
As shown in Fig. 6, the probability of a DT fusion reaction is the greatest when the nuclei’s kinetic energy is about 100 Kev (≈1,000 million degrees). Even at this optimum energy, the nuclei are much more likely to elastically scatter than to fuse! Therefore, deuterium and tritium nuclei must be confined in the reactor long enough for the fusion reaction to happen. Due to the Maxwellian distribution of the energy of the nuclei, it turns out that an average temperature of “only” 10 KeV (≈100 million degrees) is necessary in a fusion reactor. This temperature is six times the temperature at the center of the sun. The fuel must then be heated to temperatures around 100 million degrees at which the nuclei overcome the force of repulsion of the positive charges when they collide, and fuse. At much lower temperatures (about 10 thousand degrees), the electrons and nuclei separate and create an ionized gas called plasma. How to stably confine this plasma at extreme temperatures and pressures for long periods of time is the big challenge of nuclear fusion.
What is a Plasma?
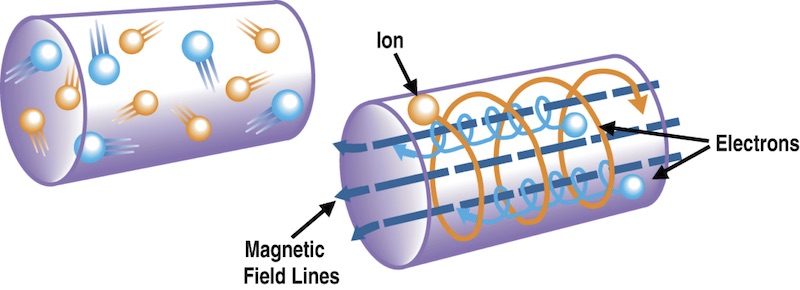
Plasmas are also known as the fourth state of matter. The other three states are solids, liquids, and gases. Each atom in a solid, liquid or gas is electrically neutral, with a positively charged nucleus surrounded by negatively charged electrons. In a plasma, the electrons are stripped from the nuclei of the atoms resulting in an ionized gas where positively and negatively charged particles move independently. Importantly, the particles in a plasma are charged, conduct electricity and interact with magnetic fields (see Fig. 7).
The difficulty in producing fusion energy has been to develop a device which can heat the fuel to a sufficiently high temperature and then confine it for a long enough time so that more energy is released through fusion reactions than is used for heating. There are three known ways to accomplish this: a- with gravitational confinement - the method that the sun uses, b- with inertial confinement - essentially imploding the hydrogen gases together with inertia then holding them together long enough for fusion reactions to occur, c- by magnetic confinement - use of magnetic fields acting on hydrogen atoms which have been ionized, i.e., given a charge, so that magnetic fields can exert a force on the particles. Both inertial and magnetic confinement approaches are actively pursued by the scientific community. The work by the LU Plasma Control Laboratory focuses on magnetic confinement. Magnetic-confinement fusion exploits the capability of the plasma to interact with magnetic fields. As shown in Fig. 7, in the presence of a prescribed magnetic field, a charged particle will describe a simple cyclotron gyration around the magnetic field line. The dynamics of the charged particle is determined by the Lorentz force,
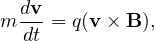
|
(4) |
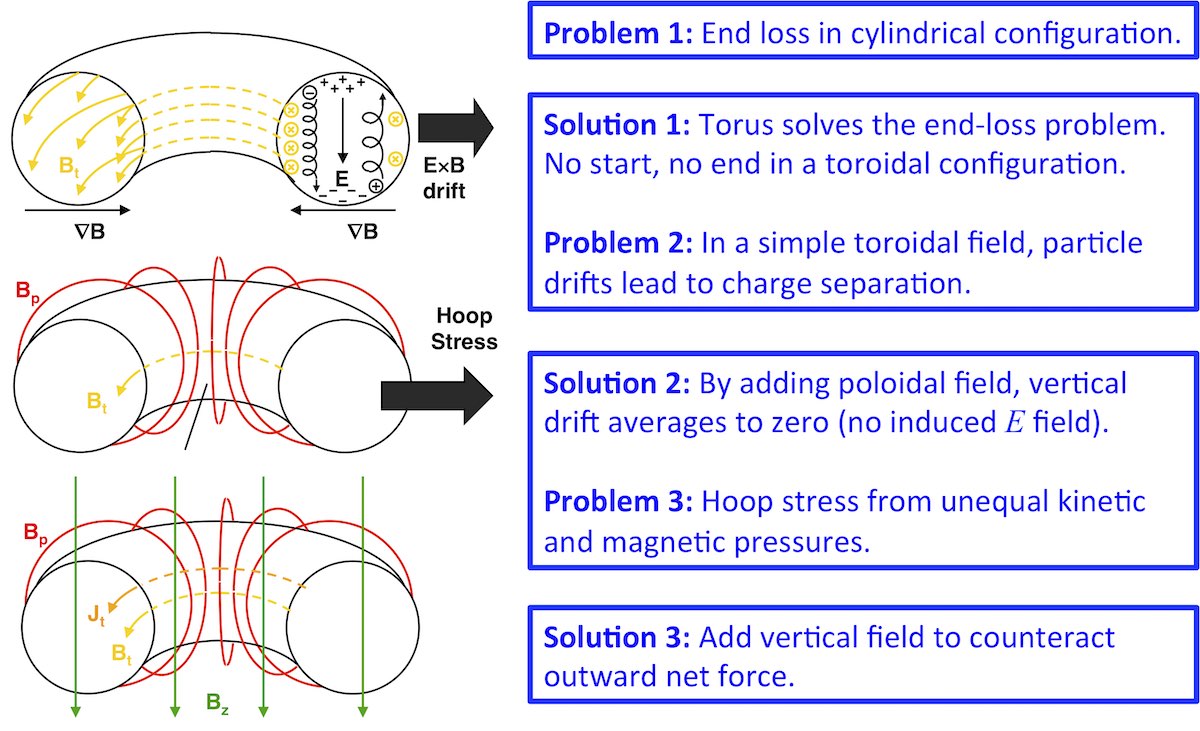
where m and q are the mass and charge of the particle respectively, v is the particle velocity, and B is the magnetic field. When the component of the velocity parallel to the magnetic field, which is not affected by the Lorentz force, is different from zero, the trajectory of the charged particle is a helix. It is in this case that the particle would fall out the ends of the magnetic field line, contrary to our desired to keep them confined. To solve this, the field lines can be bent into a torus so that there is no end as shown in Fig. 8. However, as it will be explained below, the way the toroidal field Bt is generated leads to a stronger magnetic field at the inner side of the torus and a weaker magnetic fields at its outer side. This leads to a gradient of the magnetic field pointing inwards as shown in Fig. 8. It is possible to show that this gradient in the toroidal magnetic field produces a separation of charges and the subsequent creation of an electric field E in the vertical direction. The interaction between the toroidal magnetic field and the vertical electric field finally produces an E × B drift based on the Lorentz force, which pushes the particles outward. This problem is solved by adding a poloidal component Bp of the magnetic field, which averages the vertical separation of charge to zero and prevents the creation of a vertical electrical field. This combination of toroidal and poloidal magnetic fields needs to be finally combined with a vertical component Bz of the magnetic field. The interaction of the vertical magnetic field Bz with the current Jt flowing toroidally in the plasma produces a Lorentz force that balances the ”hoop” force cause by the unequal kinetic and magnetic (lower magnetic field strength and larger area in the outer half of the torus than in the inner half of the torus) pressures.
What is a Tokamak?
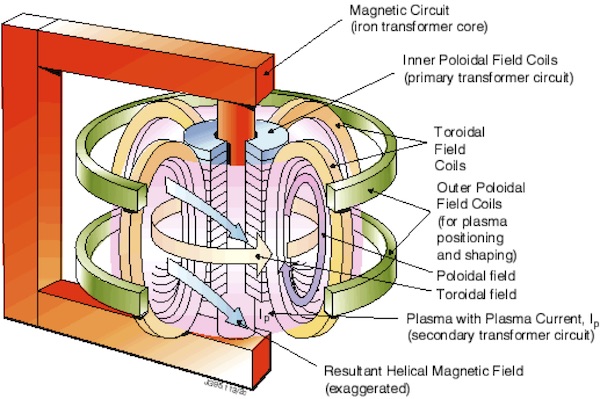
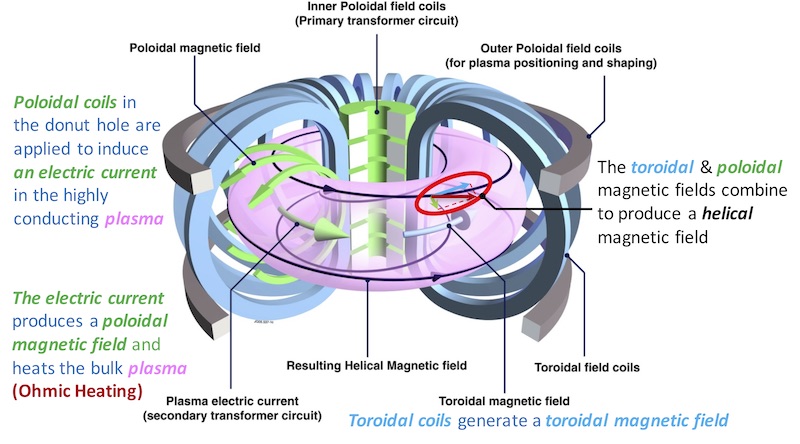
The tokamak concept invented in the Soviet Union in the late 1950’s is now the major and most promising magnetic confinement approach being pursued around the world. Tokamak is an acronym developed from the Russian words TOroidalnaya KAmera ee MAgnitaya Katushka which means “toroidal chamber with magnetic coils”. The largest tokamak in the world is the Joint European Torus (JET) in Culham, England, shown in Fig. 9.
In a tokamak, the toroidal magnetic field is produced by the so-called “toroidal field” (TF) coils. Addition of a poloidal field generated by the toroidal plasma current, which is necessary for the existence of a magnetohydrodynamic (MHD) equilibrium, produces a combined field in which the magnetic field lines twist their way around the tokamak to form a helical structure.
Fig. 10 shows an illustration of the coil distribution in the JET tokamak. The toroidal component of the magnetic field, used to confine the plasma within the torus, is generated by large D-shaped coils (toroidal field coils) with copper windings, which are equally spaced around the machine. The primary winding (inner poloidal field coils) of the transformer, used to induce the plasma current which generates the poloidal component of the field and heats the plasma, is situated at the center of the machine. Coupling between the primary winding and the toroidal plasma, acting as the single turn secondary, is enhanced by the massive eight limbed transformer core. Around the outside of the machine, but within the confines of the transformer limbs, is the set of field coils (outer poloidal field coils) used for positioning, shaping and stabilizing the position of the plasma inside the vessel. The plasma inside the torus essentially constitutes a big fat wire, since it is made up of charged particles in motion, i.e., it has a current. The large current carrying coils on the outside of the torus push or pull against the plasma based on a version of the basic principle of forces between parallel conductors. If the currents are in the same direction, the magnetic fields exert a force so as to push the wires together. If the currents are in opposite directions, the force exerted tends to push them apart. Fig. 11 offers an alternative illustration of the tokamak configuration.
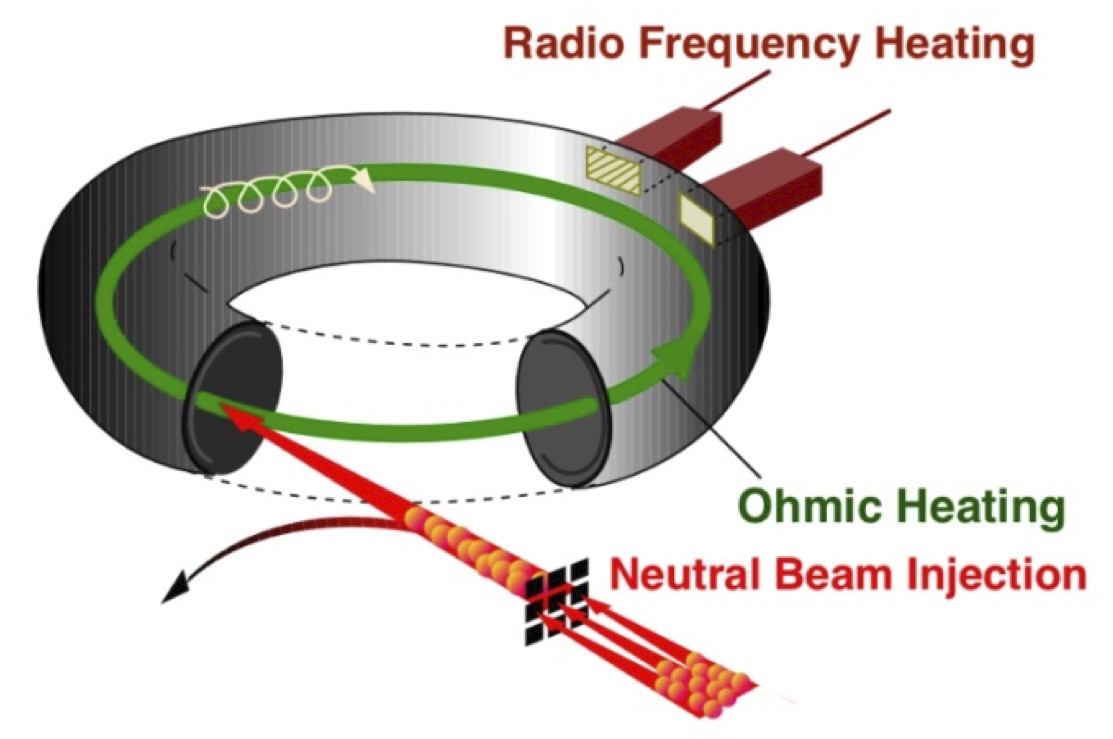
The use of transformer action for producing the large plasma current means that present tokamaks operate in a pulsed mode. Each one of the tokamak pulses is called discharge. To initiate the discharge, hydrogen gas is puffed into the tokamak vacuum vessel, the toroidal field coil current is brought up early to create a steady state magnetic field to contain the plasma when initially created, and the ohmic-heating/current-drive poloidal field coil is brought to its maximum positive current in preparation for pulse initiation. Then, the ohmic-heating/current-drive poloidal field coil current is driven down very quickly in order to produce a large electric field within the torus. This electric field rips apart the neutral gas atoms and produces the plasma. Thus, immediately after plasma initiation, the ohmic heating/current drive poloidal field coil current is commanded to continue its downward ramp so that it now operates as the primary side of a transformer whose secondary is the conductive plasma. This causes current to flow in the plasma via the exchange of charges between free ions and electrons.
The collisions of the ions make the plasma resistive. It is this resistance that heats up the plasma (thus the origin of the term “ohmic heating”). When the temperature increases, the resistance decreases and the ohmic heating loses effectiveness. To significantly increase fusion reactions, the temperature must be increased to over 100 million degrees. This heating is accomplished by particle beams (injecting energetic ions) or by radio frequency or microwaves (heating ions or electrons) as shown in Fig. 12). Shortly after the discharge starts, additional gas is puffed into the chamber to increase the density and/or pressure to desired levels. To be an economical viable source of energy, tokamaks must operate in the future in truly steady-state or at least with a succession of sufficiently long pulses. This will demand the replacement of the inductive current by non-inductive current, which could be generated by a combination of self-generated bootstrap current and current driven by neutral beam and radio frequency sources (see Fig. 12).
How is Electricity Created?
The DT reaction is the most promising fusion reaction because it requires the smallest input energy (~ 10KeV) or lowest temperature (~ 108 degrees), and yields one of the largest output energy (17.6 MeV). The energy gain for this type of reaction is around 2,000. The D-T fusion reaction produces neutrons which escape from the magnetic field due to their lack of charge and carry 80% (14.1 MeV) of the fusion energy to a specially designed wall, called the blanket. In a working power plant, as illustrated in Fig. 13, the blanket would capture the neutrons, convert their kinetic energy into the heat which drives the electrical generators, and breed the tritium fuel. The other 20% (3.5 MeV) of the fusion energy is released in helium ions or “alpha particles”, which are contained by the magnetic field and which self-heat the plasma. If conditions are right, then the plasma can produce enough fusion power so it heats itself, a so-called “burning plasma”, without requiring any auxiliary power.
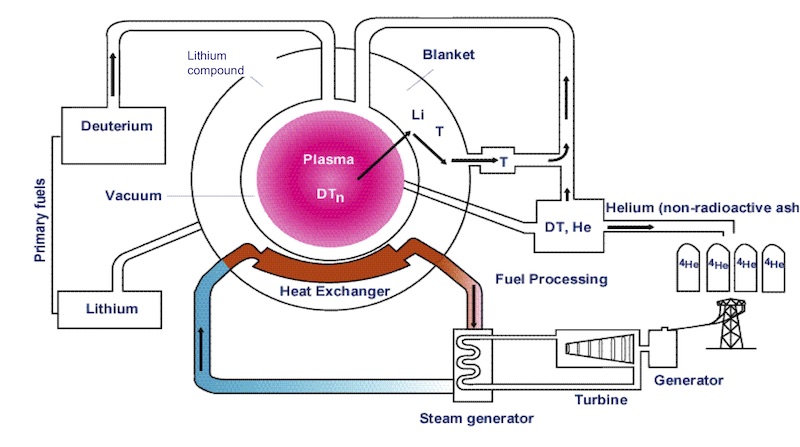
Figure 13: Fueling cycle and electricity generation in a deuterium-tritium fusion power reactor. The neutron from the DT reaction, which carries 14.1 MeV of kinetic energy, has two missions: 1- heating up of the blanket to produce steam in the primary of a heat exchanger, 2- breeding of tritium from the lithium compound. The alpha particle from the DT reaction, which carries 3.5 MeV of kinetic energy, is used to heat up the plasma and sustain the needed conditions for nuclear fusion.